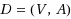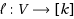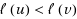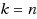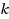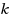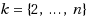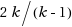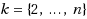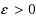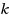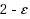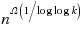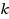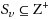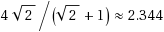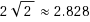On the Approximability of Digraph Ordering

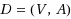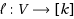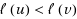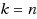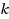Given an n‐vertex digraph $D=(V,A)$ the Max‐ $k$ ‐Ordering problem is to compute a labeling $𝓁:V\to [k]$ maximizing the number of forward edges, i.e. edges (u, v) such that $𝓁(u)<𝓁(v)$ . For different values of k, this reduces to maximum acyclic subgraph ( $k=n$ ), and Max‐DiCut ( $k=2$ ). This work studies the approximability of Max‐ $k$ ‐Ordering and its generalizations, motivated by their applications to job scheduling with soft precedence constraints. We give an LP rounding based 2‐approximation algorithm for Max‐ 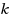$k$ ‐Ordering for any 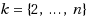$k=\{2,\dots ,n\}$ , improving on the known 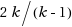$2k/(k‐1)$ ‐approximation obtained via random assignment. 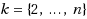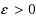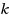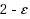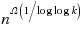The tightness of this rounding is shown by proving that for any $k=\{2,\dots ,n\}$ and constant $\mathit{ϵ}>0$ , Max‐ $k$ ‐Ordering has an LP integrality gap of $2‐\mathit{ϵ}$ for $n^{\mathit{\Omega }\left(1/loglogk\right)}$ rounds of the Sherali‐Adams hierarchy. A further generalization of Max‐ 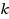$k$ ‐Ordering is the restricted maximum acyclic subgraph problem or RMAS, where each vertex v has a finite set of allowable labels 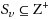$S_v\subseteq {‐{Z}}^{+}$ . We prove an LP rounding based 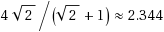$4\sqrt{2}/\left(\sqrt{2}+1\right)\approx 2.344$ approximation for it, improving on the 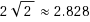$2\sqrt{2}\approx 2.828$ approximation recently given by Grandoni et al. (Inf Process Lett 115(2): 182–185, 2015). In fact, our approximation algorithm also works for a general version where the objective counts the edges which go forward by at least a positive offset specific to each edge. The minimization formulation of digraph ordering is DAG edge deletion or DED 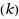$(k)$ , which requires deleting the minimum number of edges from an n‐vertex directed acyclic graph (DAG) to remove all paths of length k. We show that a simple rounding of the LP relaxation as well as a local ratio approach for DED 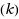$(k)$ yields k‐approximation for any $k\in [n]$ . A vertex deletion version was studied earlier by Paik et al. (IEEE Trans Comput 43(9): 1091–1096, 1994), and Svensson (Proceedings of the APPROX, 2012).