We study connectivity relations among points, where the precise location of each input point lies in a region of uncertainty. We distinguish two fundamental scenarios under which uncertainty arises. In the favorable Best‐Case Uncertainty, each input point can be chosen from a given set to yield the best possible objective value. In the unfavorable Worst‐Case Uncertainty, the input set has worst possible objective value among all possible point locations, which are uncertain due, for example, to imprecise data. We consider these notions of uncertainty for the bottleneck spanning tree problem, giving rise to the following Best‐Case Connectivity with Uncertainty problem: given a family of geometric regions, choose one point per region, such that the longest edge length of an associated geometric spanning tree is minimized. We show that this problem is NP‐hard even for very simple scenarios in which the regions are line segments or squares. On the other hand, we give an exact solution for the case in which there are
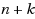regions, where k of the regions are line segments and n of the regions are fixed points. We then give approximation algorithms for cases where the regions are either all line segments or all unit discs. We also provide approximation methods for the corresponding Worst‐Case Connectivity with Uncertainty problem: Given a set of uncertainty regions, find the minimal distance r such that for any choice of points, one per region, there is a spanning tree among the points with edge length at most r.
