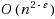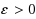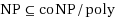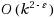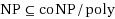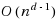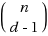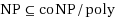| Article ID: | iaor20173020 |
| Volume: | 79 |
| Issue: | 1 |
| Start Page Number: | 3 |
| End Page Number: | 28 |
| Publication Date: | Sep 2017 |
| Journal: | Algorithmica |
| Authors: | Jansen Bart |
| Keywords: | graphs, heuristics |
We present several sparsification lower and upper bounds for classic problems in graph theory and logic. For the problems 4‐