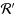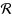Extending Partial Representations of Interval Graphs

Interval graphs are intersection graphs of closed intervals of the real‐line. The well‐known computational problem, called recognition, asks whether an input graph G can be represented by closed intervals, i.e., whether G is an interval graph. There are several linear‐time algorithms known for recognizing interval graphs, the oldest one is by Booth and Lueker (J Comput Syst Sci 13:335–379, 1976) based on PQ‐trees. In this paper, we study a generalization of recognition, called partial representation extension. The input of this problem consists of a graph G with a partial representation 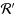${\mathcal{R}}^{\prime }$ fixing the positions of some intervals. The problem asks whether it is possible to place the remaining interval and create an interval representation 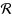$\mathcal{R}$ of the entire graph G extending ${\mathcal{R}}^{\prime }$ . We generalize the characterization of interval graphs by Fulkerson and Gross (Pac J Math 15:835–855, 1965) to extendible partial representations. Using it, we give a linear‐time algorithm for partial representation extension based on a reordering problem of PQ‐trees.