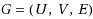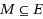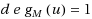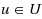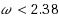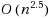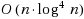| Article ID: | iaor20173016 |
| Volume: | 78 |
| Issue: | 3 |
| Start Page Number: | 896 |
| End Page Number: | 913 |
| Publication Date: | Jul 2017 |
| Journal: | Algorithmica |
| Authors: | Galk Frantiek, Katreni Jn, Semaniin Gabriel |
| Keywords: | graphs, heuristics |
A