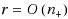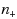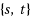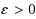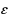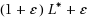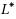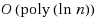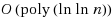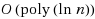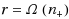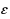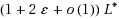Braess’s paradox states that removing a part of a network may improve the players’ latency at equilibrium. In this work, we study the approximability of the best subnetwork problem for the class of random
 instances proven prone to Braess’s paradox by Valiant and Roughgarden RSA ‘10 (Random Struct Algorithms 37(4):495–515, 2010), Chung and Young WINE ‘10 (LNCS 6484:194–208, 2010) and Chung et al. RSA ‘12 (Random Struct Algorithms 41(4):451–468, 2012). Our main contribution is a polynomial‐time approximation‐preserving reduction of the best subnetwork problem for such instances to the corresponding problem in a simplified network where all neighbors of source s and destination t are directly connected by 0 latency edges. Building on this, we consider two cases, either when the total rate r is sufficiently low, or, when r is sufficiently high. In the first case of low
instances proven prone to Braess’s paradox by Valiant and Roughgarden RSA ‘10 (Random Struct Algorithms 37(4):495–515, 2010), Chung and Young WINE ‘10 (LNCS 6484:194–208, 2010) and Chung et al. RSA ‘12 (Random Struct Algorithms 41(4):451–468, 2012). Our main contribution is a polynomial‐time approximation‐preserving reduction of the best subnetwork problem for such instances to the corresponding problem in a simplified network where all neighbors of source s and destination t are directly connected by 0 latency edges. Building on this, we consider two cases, either when the total rate r is sufficiently low, or, when r is sufficiently high. In the first case of low
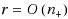 , here
, here
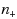 is the maximum degree of
is the maximum degree of
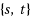 , we obtain an approximation scheme that for any constant
, we obtain an approximation scheme that for any constant
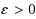 and with high probability, computes a subnetwork and an
and with high probability, computes a subnetwork and an
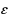 ‐Nash flow with maximum latency at most
‐Nash flow with maximum latency at most
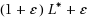 , where
, where
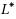 is the equilibrium latency of the best subnetwork. Our approximation scheme runs in polynomial time if the random network has average degree
is the equilibrium latency of the best subnetwork. Our approximation scheme runs in polynomial time if the random network has average degree
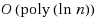 and the traffic rate is
and the traffic rate is
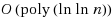 , and in quasipolynomial time for average degrees up to o(n) and traffic rates of
, and in quasipolynomial time for average degrees up to o(n) and traffic rates of
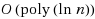 . Finally, in the second case of high
. Finally, in the second case of high
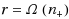 , we compute in strongly polynomial time a subnetwork and an
, we compute in strongly polynomial time a subnetwork and an
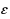 ‐Nash flow with maximum latency at most
‐Nash flow with maximum latency at most
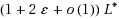 .
.