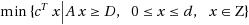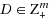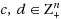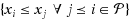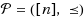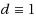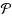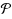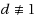A covering problem is an integer linear program of type
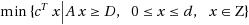 where
where
 ,
,
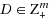 , and
, and
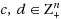 . In this paper, we study covering problems with additional precedence constraints
. In this paper, we study covering problems with additional precedence constraints
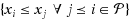 , where
, where
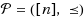 is some arbitrary, but fixed partial order on the items represented by the column‐indices of A. Such precedence constrained covering problems (PCCPs) are of high theoretical and practical importance even in the special case of the precedence constrained knapsack problem, that is, where
is some arbitrary, but fixed partial order on the items represented by the column‐indices of A. Such precedence constrained covering problems (PCCPs) are of high theoretical and practical importance even in the special case of the precedence constrained knapsack problem, that is, where
 and
and
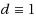 . Our main result is a strongly‐polynomial primal–dual approximation algorithm for PCCP with
. Our main result is a strongly‐polynomial primal–dual approximation algorithm for PCCP with
 . Our approach generalizes the well‐known knapsack cover inequalities to obtain an IP formulation which renders any explicit precedence constraints redundant. The approximation ratio of this algorithm is upper bounded by the width of
. Our approach generalizes the well‐known knapsack cover inequalities to obtain an IP formulation which renders any explicit precedence constraints redundant. The approximation ratio of this algorithm is upper bounded by the width of
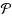 , that is, by the size of a maximum antichain in
, that is, by the size of a maximum antichain in
 . Interestingly, this bound is independent of the number of constraints. We are not aware of any other results on approximation algorithms for PCCP on arbitrary posets
. Interestingly, this bound is independent of the number of constraints. We are not aware of any other results on approximation algorithms for PCCP on arbitrary posets
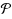 . For the general case with
. For the general case with
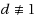 , we present pseudo‐polynomial algorithms. Finally, we show that the problem does not admit a PTAS under standard complexity assumptions.
, we present pseudo‐polynomial algorithms. Finally, we show that the problem does not admit a PTAS under standard complexity assumptions.