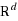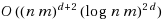FPTAS for Minimizing the Earth Mover’s Distance Under Rigid Transformations and Related Problems

In this paper, we consider the problem (denoted as EMDRT) of minimizing the earth mover’s distance between two sets of weighted points A and B in 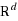${‐{R}}^d$ under rigid transformation. EMDRT is an important problem in both theory and applications and has received considerable attentions in recent years. Previous research on this problem has resulted in only constant factor approximations and it has been an open problem for a long time to achieve PTAS solution. In this paper, we present the first FPTAS algorithm for EMDRT. Our algorithm runs roughly in 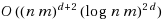$O({(nm)}^{d+2}{(lognm)}^{2d})$ time (which is close to a lower bound on any PTAS for this problem), where n and m are the sizes of A and B, respectively. Our result is based on several new techniques, such as the Sequential Orthogonal Decomposition and Optimum Guided Base, and can be extended to several related problems, such as the problem of earth mover’s distance under similarity transformation and the alignment problem, to achieve FPTAS for each of them.