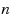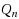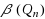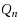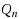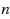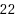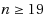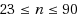| Article ID: | iaor20172919 |
| Volume: | 11 |
| Issue: | 6 |
| Start Page Number: | 1057 |
| End Page Number: | 1067 |
| Publication Date: | Aug 2017 |
| Journal: | Optimization Letters |
| Authors: | Cangalovic Mirjana, Nikolic Neboja, Grujicic Igor |
| Keywords: | graphs, heuristics, combinatorial optimization, programming: dynamic |
In this paper we consider some special characteristics of distances between vertices in the