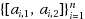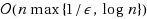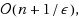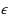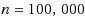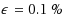A new fully polynomial time approximation scheme for the interval subset sum problem

The interval subset sum problem (ISSP) is a generalization of the well‐known subset sum problem. Given a set of intervals 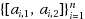${\left\{[a_{i,1},a_{i,2}]\right\}}_{i=1}^n$ and a target integer T, the ISSP is to find a set of integers, at most one from each interval, such that their sum best approximates the target T but cannot exceed it. In this paper, we first study the computational complexity of the ISSP. We show that the ISSP is relatively easy to solve compared to the 0–1 knapsack problem. We also identify several subclasses of the ISSP which are polynomial time solvable (with high probability), albeit the problem is generally NP‐hard. Then, we propose a new fully polynomial time approximation scheme for solving the general ISSP problem. 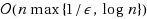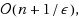The time and space complexities of the proposed scheme are $\mathcal{O}\left(nmax\left\{1/\mathit{ϵ},logn\right\}\right)$ and $\mathcal{O}\left(n+1/\mathit{ϵ}\right),$ respectively, where 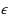$\mathit{ϵ}$ is the relative approximation error. To the best of our knowledge, the proposed scheme has almost the same time complexity but a significantly lower space complexity compared to the best known scheme. Both the correctness and efficiency of the proposed scheme are validated by numerical simulations. 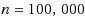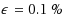In particular, the proposed scheme successfully solves ISSP instances with $n=100,000$ and $\mathit{ϵ}=0.1\%$ within 1 s.