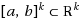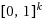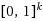A new global optimization method for a symmetric Lipschitz continuous function and the application to searching for a globally optimal partition of a one-dimensional set

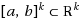In this paper, we consider a global optimization problem for a symmetric Lipschitz continuous function $g:{[a,b]}^k\to ‐{R}$ , whose domain ${[a,b]}^k\subset {‐{R}}^k$ consists of k! hypertetrahedrons of the same size and shape, in which function g attains equal values. A global minimum can therefore be searched for in one hypertetrahedron only, but then this becomes a global optimization problem with linear constraints. Apart from that, some known global optimization algorithms in standard form cannot be applied to solving the problem. In this paper, it is shown how this global optimization problem with linear constraints can easily be transformed into a global optimization problem on hypercube 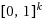${[0,1]}^k$ , for the solving of which an applied DIRECT algorithm in standard form is possible. This approach has a somewhat lower efficiency than known global optimization methods for symmetric Lipschitz continuous functions (such as SymDIRECT or DISIMPL), but, on the other hand, this method allows for the use of publicly available and well developed computer codes for solving a global optimization problem on hypercube 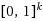${[0,1]}^k$ (e.g. the DIRECT algorithm). The method is illustrated and tested on standard symmetric functions and very demanding center‐based clustering problems for the data that have only one feature. An application to the image segmentation problem is also shown.