Global probability maximization for a Gaussian bilateral inequality in polynomial time

The present paper investigates Gaussian bilateral inequalities in view of solving related probability maximization problems. Since the function f representing the probability of satisfaction of a given Gaussian bilateral inequality is not concave everywhere, we first state and prove a necessary and sufficient condition for negative semi‐definiteness of the Hessian. Then, the (nonconvex) problem of globally maximizing f over a given polyhedron in 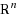${‐{R}}^n$ is adressed, and shown to be polynomial‐time solvable, thus yielding a new‐comer to the (short) list of nonconvex global optimization problems which can be solved exactly in polynomial time. Application to computing upper bounds to the maximum joint probability of satisfaction of a set of m independent Gaussian bilateral inequalities is discussed and computational results are reported.