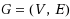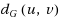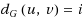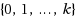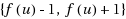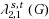A note on (s, t)-relaxed L(2, 1)-labeling of graphs

Let 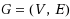$G=(V,E)$ be a graph. For two vertices u and v in G, we denote 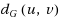$d_G(u,v)$ the distance between u and v. A vertex v is called an i‐neighbor of u if 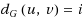$d_G(u,v)=i$ . Let s, t and k be nonnegative integers. An (s, t)‐relaxed k‐L(2, 1)‐labeling of a graph G is an assignment of labels from 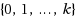$\{0,1,\dots ,k\}$ to the vertices of G if the following three conditions are met: (1) adjacent vertices get different labels; (2) for any vertex u of G, there are at most s 1‐neighbors of u receiving labels from 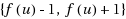$\{f(u)‐1,f(u)+1\}$ ; (3) for any vertex u of G, the number of 2‐neighbors of u assigned the label f(u) is at most t. The (s, t)‐relaxed L(2, 1)‐labeling number 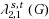${\mathit{\lambda }}_{2,1}^{s,t}(G)$ of G is the minimum k such that G admits an (s, t)‐relaxed k‐L(2, 1)‐labeling. In this article, we refute Conjecture 4 and Conjecture 5 stated in (Lin in J Comb Optim. doi: 10.1007/s10878‐014‐9746-9, 2013).