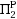Graph pebbling is a network model for studying whether or not a given supply of discrete pebbles can satisfy a given demand via pebbling moves. A pebbling move across an edge of a graph takes two pebbles from one endpoint and places one pebble at the other endpoint; the other pebble is lost in transit as a toll. It has been shown that deciding whether a supply can meet a demand on a graph is NP‐complete. The pebbling number of a graph is the smallest t such that every supply of t pebbles can satisfy every demand of one pebble byt a vertex. Deciding if the pebbling number is at most k is
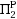‐complete. In this paper we develop a tool, called the Weight Function Lemma, for computing upper bounds and sometimes exact values for pebbling numbers with the assistance of linear optimization. With this tool we are able to calculate the pebbling numbers of much larger graphs than in previous algorithms, and much more quickly as well. We also obtain results for many families of graphs, in many cases by hand, with much simpler and remarkably shorter proofs than given in previously existing arguments (certificates typically of size at most the number of vertices times the maximum degree), especially for highly symmetric graphs. Here we apply the Weight Function Lemma to several specific graphs, including the Petersen, Lemke,
weak Bruhat, and Lemke squared, as well as to a number of infinite families of graphs, such as trees, cycles, graph powers of cycles, cubes, and some generalized Petersen and Coxeter graphs. In doing so we partly answer a question of Pachter, et al., by computing the pebbling exponent of cycles to within an asymptotically small range. It is conceivable that this method yields an approximation algorithm for graph pebbling.
