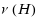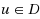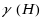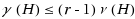| Article ID: | iaor20172791 |
| Volume: | 34 |
| Issue: | 2 |
| Start Page Number: | 656 |
| End Page Number: | 659 |
| Publication Date: | Aug 2017 |
| Journal: | Journal of Combinatorial Optimization |
| Authors: | Kang Liying, Shan Erfang, Li Shan, Dong Yanxia |
| Keywords: | combinatorial optimization, graphs, heuristics |
A matching is a set of pairwise disjoint hyperedges of a hypergraph