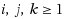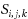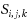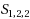Independent sets in some classes of Si,j,k-free graphs

The maximum weight independent set (MWIS) problem on graphs with vertex weights asks for a set of pairwise nonadjacent vertices of maximum total weight. In 1982, Alekseev (Comb Algebraic Methods Appl Math 132:3–13, 1982) showed that the M(W)IS problem remains NP‐complete on H‐free graphs, whenever H is connected, but neither a path nor a subdivision of the claw. We will focus on graphs without a subdivision of a claw. For integers $i,j,k\ge 1$ , let $S_{i,j,k}$ denote a tree with exactly three vertices of degree one, being at distance i, j and k from the unique vertex of degree three. Note that $S_{i,j,k}$ is a subdivision of a claw. The computational complexity of the MWIS problem for the class of $S_{1,2,2}$ ‐free graphs, and for the class of $S_{1,1,3}$ ‐free graphs are open. In this paper, we show that the MWIS problem can be solved in polynomial time for ( $S_{1,2,2},S_{1,1,3}$ , co‐chair)‐free graphs, by analyzing the structure of the subclasses of this class of graphs. This also extends some known results in the literature.