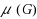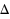| Article ID: | iaor20172787 |
| Volume: | 34 |
| Issue: | 2 |
| Start Page Number: | 574 |
| End Page Number: | 587 |
| Publication Date: | Aug 2017 |
| Journal: | Journal of Combinatorial Optimization |
| Authors: | Das Kinkar, Nadjafi-Arani M |
| Keywords: | combinatorial optimization, graphs, heuristics |
Let