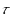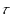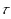Two efficient values of cooperative games with graph structure based on τ-values

The paper is devoted to value concepts for cooperative games with a communication structure represented by a graph. Under assumptions that the players partition themselves into ‘components’ before realizing cooperation and the worth of the grand coalition not less than the sum of the worths of all components, the fair distribution of surplus solution and the two‐step $\mathit{\tau }$ ‐value are introduced as two efficient values for such games, each of which is an extension of the graph $\mathit{\tau }$ ‐value. For the two efficient values, we discuss their special properties and we provide their axiomatic characterizations in views of those properties. By analysing an example applied to the two values, we conclude that the fair distribution of surplus solution allocates more surplus to the bigger coalitions and favors the powerful players, while the two‐step $\mathit{\tau }$ ‐value benefits the vulnerable groups and inspires to form small coalitions.