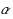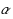An extension principle based solution approach for shortest path problem with fuzzy arc lengths

A shortest path problem on a network in the presence of fuzzy arc lengths is focused in this paper. The aim is to introduce the shortest path connecting the first and last vertices of the network which has minimum fuzzy sum of arc lengths among all possible paths. In this study a solution algorithm based on the extension principle of Zadeh is developed to solve the problem. The algorithm decomposes the fuzzy shortest path problem into two lower bound and upper bound sub‐problems. Each sub‐problem is solved individually in different $\mathit{\alpha }$ levels to obtain the shortest path, its fuzzy length and its associated membership function value. The proposed method contains no fuzzy ranking function and also for each $\mathit{\alpha }$ ‐cut, it gives a unique lower and upper bound for the fuzzy length of the shortest path. The algorithm is examined over some well‐known networks from the literature and its performance is superior to the existent methods.