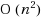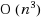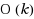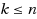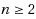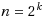| Article ID: | iaor20172740 |
| Volume: | 254 |
| Issue: | 1 |
| Start Page Number: | 37 |
| End Page Number: | 46 |
| Publication Date: | Jul 2017 |
| Journal: | Annals of Operations Research |
| Authors: | Eli Haluk |
| Keywords: | graphs, combinatorial optimization, heuristics, programming: integer |
1.5 dimensional (1.5D) terrain is characterized by a piecewise linear curve. Locating minimum number of guards on the terrain (