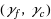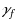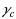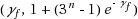| Article ID: | iaor20171793 |
| Volume: | 11 |
| Issue: | 5 |
| Start Page Number: | 983 |
| End Page Number: | 993 |
| Publication Date: | Jun 2017 |
| Journal: | Optimization Letters |
| Authors: | Xu Dachuan, Du Donglei, Wang Yishui, Wu Chenchen |
| Keywords: | combinatorial optimization, facilities |
We consider the