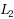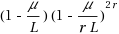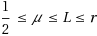Accelerated parallel and distributed algorithm using limited internal memory for nonnegative matrix factorization

Nonnegative matrix factorization (NMF) is a powerful technique for dimension reduction, extracting latent factors and learning part‐based representation. For large datasets, NMF performance depends on some major issues such as fast algorithms, fully parallel distributed feasibility and limited internal memory. This research designs a fast fully parallel and distributed algorithm using limited internal memory to reach high NMF performance for large datasets. Specially, we propose a flexible accelerated algorithm for NMF with all its $L_1$ $L_2$ regularized variants based on full decomposition, which is a combination of exact line search, greedy coordinate descent, and accelerated search. The proposed algorithm takes advantages of these algorithms to converges linearly at an over‐bounded rate $(1‐\frac{\mathit{\mu }}{L}){(1‐\frac{\mathit{\mu }}{rL})}^{2r}$ in optimizing each factor matrix when fixing the other factor one in the sub‐space of passive variables, where r is the number of latent components, and $\mathit{\mu }$ and L are bounded as $\frac{1}{2}\le \mathit{\mu }\le L\le r$ . In addition, the algorithm can exploit the data sparseness to run on large datasets with limited internal memory of machines, which is is advanced compared to fast block coordinate descent methods and accelerated methods. Our experimental results are highly competitive with seven state‐of‐the‐art methods about three significant aspects of convergence, optimality and average of the iteration numbers.