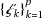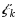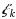| Article ID: | iaor20171752 |
| Volume: | 68 |
| Issue: | 2 |
| Start Page Number: | 279 |
| End Page Number: | 306 |
| Publication Date: | Jun 2017 |
| Journal: | Journal of Global Optimization |
| Authors: | Seeger Alberto, Vidal -Nuez Jos |
| Keywords: | heuristics |
Consider a finite collection