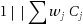An examination of job interchange relationships and induction-based proofs in single machine scheduling

We provide a generalization of Lawler’s (Mathematical programming the state of the art. Springer, Berlin, pp 202–234, 1983) Theorem on solutions to permutation scheduling problems when the objective function admits a particular job interchange relation. We complete Lawler’s result with a straight‐forward proof by induction on n, the number of jobs. A notable application is $1||\mathit{\sum }{w}_j{C}_j$ where the objective of total weighted completion time admits WSPT (i.e., scheduling jobs in non‐decreasing order of $p_j/w_j$ ). We provide new proofs by induction for the optimality of WSPT as well as for SPT in the unweighted case.