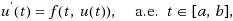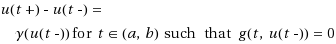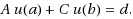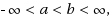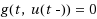A constructive approach to boundary value problems with state-dependent impulses

We investigate the non‐linear system of ordinary differential equations 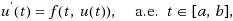$u^{\text{'}}\left(t\right)=f(t,u\left(t\right)),\text{a.e.}t\in [a,b],$ subject to the state‐dependent impulse condition 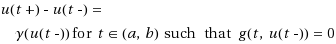$u(t+)‐u(t‐)=\gamma \left(u\right(t‐\left)\right)\text{for}t\in (a,b)\text{such}\text{that}g(t,u(t‐\left)\right)=0$ and the linear two‐point boundary condition 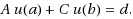$Au\left(a\right)+Cu\left(b\right)=d.$ Here, $-\infty <a<b<\infty ,$ 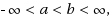f and γ are given continuous vector‐functions, g is a continuous scalar function, A, C are constant matrices, and d is a constant vector. The instants of time t where the jump occurs are determined by the equation 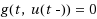$g(t,u(t‐\left)\right)=0$ and, thus, are unknown a priori and essentially depend on the solution u. We discuss a reduction technique allowing one to combine the analysis of existence of solutions with an efficient construction of approximate solutions. At present, according to the authors’ knowledge, no numerical results for boundary value problems with state‐dependent impulses are available in the literature.