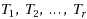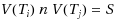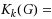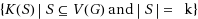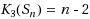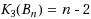For S ⊆ G, let K(S) denote the maximum number r of edge‐disjoint trees
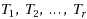 in G such that
in G such that
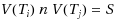 for any
for any
 and i ≠ j. For every 2 ≤ k ≤ n, the generalized k‐connectivity of G Kk
(G) is defined as the minimum K(S) over all k‐subsets S of vertices, i.e.,
and i ≠ j. For every 2 ≤ k ≤ n, the generalized k‐connectivity of G Kk
(G) is defined as the minimum K(S) over all k‐subsets S of vertices, i.e.,
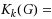 min
min
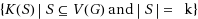 . Clearly, K
2(G) corresponds to the traditional connectivity of G. The generalized k‐connectivity can serve for measuring the capability of a network G to connect any k vertices in G. Cayley graphs have been used extensively to design interconnection networks. In this paper, we restrict our attention to two classes of Cayley graphs, the star graphs Sn
and the bubble‐sort graphs Bn
, and investigate the generalized 3‐connectivity of Sn
and Bn
. We show that
. Clearly, K
2(G) corresponds to the traditional connectivity of G. The generalized k‐connectivity can serve for measuring the capability of a network G to connect any k vertices in G. Cayley graphs have been used extensively to design interconnection networks. In this paper, we restrict our attention to two classes of Cayley graphs, the star graphs Sn
and the bubble‐sort graphs Bn
, and investigate the generalized 3‐connectivity of Sn
and Bn
. We show that
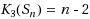 and
and
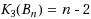 .
.