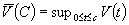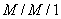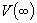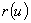| Article ID: | iaor19931609 |
| Country: | United States |
| Volume: | 8 |
| Start Page Number: | 421 |
| End Page Number: | 458 |
| Publication Date: | Nov 1992 |
| Journal: | Stochastic Models |
| Authors: | Perry David, Asmussen Soren |
| Keywords: | stochastic processes |
The distribution of the maximum