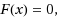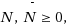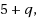In this paper, we consider the semilocal convergence on a class of improved Chebyshev–Halley type methods for solving
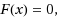 where F: Ω ⊆ X → Y is a nonlinear operator, X and Y are two Banach spaces, Ω is a non‐empty open convex subset in X. To solve the problems that F‴(x) is unbounded in Ω and it can not satisfy the whole Lipschitz or Hölder continuity, ∥F‴(x)∥ ≤ N is replaced by
where F: Ω ⊆ X → Y is a nonlinear operator, X and Y are two Banach spaces, Ω is a non‐empty open convex subset in X. To solve the problems that F‴(x) is unbounded in Ω and it can not satisfy the whole Lipschitz or Hölder continuity, ∥F‴(x)∥ ≤ N is replaced by
 for all x ∈ Ω, where
for all x ∈ Ω, where
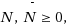 x
0 is an initial point. Moreover, F‴(x) is assumed to be local Hölder continuous. So the convergence conditions are relaxed. We prove an existence‐uniqueness theorem for the solution, which shows that the R‐order of these methods is at least
x
0 is an initial point. Moreover, F‴(x) is assumed to be local Hölder continuous. So the convergence conditions are relaxed. We prove an existence‐uniqueness theorem for the solution, which shows that the R‐order of these methods is at least
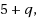 where q ∈ (0, 1]. Especially, when F‴(x) is local Lipschitz continuous, the R‐order will become six.
where q ∈ (0, 1]. Especially, when F‴(x) is local Lipschitz continuous, the R‐order will become six.