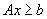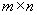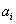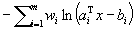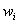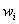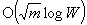| Article ID: | iaor19931566 |
| Country: | Netherlands |
| Volume: | 57 |
| Issue: | 2 |
| Start Page Number: | 163 |
| End Page Number: | 192 |
| Publication Date: | Nov 1992 |
| Journal: | Mathematical Programming |
| Authors: | Vaidya Pravin M., Atkinson David S. |
Let a bounded full dimensional polytope be defined by the system