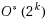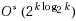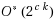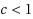Tight lower bounds for the Workflow Satisfiability Problem based on the Strong Exponential Time Hypothesis

The Workflow Satisfiability Problem (WSP) asks whether there exists an assignment of authorized users to the steps in a workflow specification, subject to certain constraints on the assignment. The problem is NP‐hard even when restricted to just not equal constraints. Since the number of steps k is relatively small in practice, Wang and Li (2010) [21] introduced a parametrisation of WSP by k. Wang and Li (2010) [21] showed that, in general, the WSP is W[1]‐hard, i.e., it is unlikely that there exists a fixed‐parameter tractable (FPT) algorithm for solving the WSP. Crampton et al. (2013) [10] and Cohen et al. (2014) [6] designed FPT algorithms of running time $O^{*}(2^k)$ and $O^{*}(2^{k{\log }_{2}k})$ for the WSP with so‐called regular and user‐independent constraints, respectively. In this note, we show that there are no algorithms of running time $O^{*}(2^{ck})$ and $O^{*}(2^{ck{\log }_{2}k})$ for the two restrictions of WSP, respectively, with any $c<1$ , unless the Strong Exponential Time Hypothesis fails.