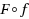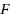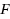Multivariate McCormick relaxations

McCormick (Math Prog 10(1):147–175, 1976) provides the framework for convex/concave relaxations of factorable functions, via rules for the product of functions and compositions of the form 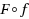$F\circ f$ , where 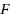$F$ is a univariate function. Herein, the composition theorem is generalized to allow multivariate outer functions 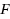$F$ , and theory for the propagation of subgradients is presented. The generalization interprets the McCormick relaxation approach as a decomposition method for the auxiliary variable method. In addition to extending the framework, the new result provides a tool for the proof of relaxations of specific functions. Moreover, a direct consequence is an improved relaxation for the product of two functions, at least as tight as McCormick’s result, and often tighter. The result also allows the direct relaxation of multilinear products of functions. Furthermore, the composition result is applied to obtain improved convex underestimators for the minimum/maximum and the division of two functions for which current relaxations are often weak. These cases can be extended to allow composition of a variety of functions for which relaxations have been proposed.