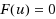Continuation Newton methods

Severely nonlinear problems can only be solved by some homotopy continuation method. An example of a homotopy method is the continuous Newton method which, however, must be discretized which leads to the damped step version of Newton’s method. The standard Newton iteration method for solving systems of nonlinear equations $F\left(u\right)=0$ must be modified in order to get global convergence, i.e. convergence from any initial point. The control of steplengths in the damped step Newton method can lead to many small steps and slow convergence. Furthermore, the applicability of the method is restricted in as much as it assumes a nonsingular and everywhere differentiable mapping $F(·)$ . Classical continuation methods are surveyed. Then a new method in the form of a coupled Newton and load increment method is presented and shown to have a global convergence already from the start and second order of accuracy with respect to the load increment step and with less restrictive regularity assumptions than for the standard Newton method. The method is applied for an elastoplastic problem with hardening.