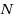Numerical stability for nonlinear evolution equations

The paper deals with discretisation methods for nonlinear operator equations written as abstract nonlinear evolution equations. Brezis and Pazy showed that the solution of such problems is given by nonlinear semigroups whose theory was founded by Crandall and Liggett. By using the approximation theorem of Brezis and Pazy, we show the $N$ ‐stability of the abstract nonlinear discrete problem for the implicit Euler method. Motivated by the rational approximation methods for linear semigroups, we propose a more general time discretisation method and prove its $N$ ‐stability as well.