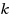Two symbolic algorithms for inverting
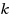 ‐tridiagonal matrices have been recently found by El‐Mikkawy and Atlan (2014, 2015). These two algorithms are mainly based on the Doolittle LU factorization of the
‐tridiagonal matrix. In the current paper, we present a new explicit analytic expression for the inverses of general tridiagonal matrices at first. By using a block diagonalization technique, we then relate
‐tridiagonal matrix inversion to tridiagonal matrix inversion. Meanwhile, an efficient algorithm is derived for computing the inverses of nonsingular
‐tridiagonal matrices with the help of any algorithm for computing the inverses of tridiagonal matrices. Three examples are given in order to illustrate the performance and efficiency of the proposed algorithms.
‐tridiagonal matrices have been recently found by El‐Mikkawy and Atlan (2014, 2015). These two algorithms are mainly based on the Doolittle LU factorization of the
‐tridiagonal matrix. In the current paper, we present a new explicit analytic expression for the inverses of general tridiagonal matrices at first. By using a block diagonalization technique, we then relate
‐tridiagonal matrix inversion to tridiagonal matrix inversion. Meanwhile, an efficient algorithm is derived for computing the inverses of nonsingular
‐tridiagonal matrices with the help of any algorithm for computing the inverses of tridiagonal matrices. Three examples are given in order to illustrate the performance and efficiency of the proposed algorithms.