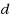| Article ID: | iaor201530127 |
| Volume: | 70 |
| Issue: | 12 |
| Start Page Number: | 3043 |
| End Page Number: | 3056 |
| Publication Date: | Dec 2015 |
| Journal: | Computers and Mathematics with Applications |
| Authors: | Wu Jianhua, Li Shanbing, Nie Hua |
| Keywords: | differential equations, matrices, numerical analysis |
We consider a diffusive Leslie–Gower predator–prey model subject to the homogeneous Neumann boundary condition. Treating the diffusion coefficient