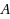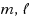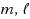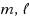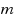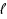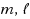A hybridized iterative algorithm of the BiCORSTAB and GPBiCOR methods for solving non-Hermitian linear systems

In this study, we derive a new iterative algorithm (including its preconditioned version) which is a hybridized variant of the biconjugate 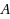$A$ ‐orthogonal residual stabilized (BiCORSTAB) method and the generalized product‐type solvers based on BiCOR (GPBiCOR) method. The proposed method, which is named GPBiCOR( 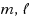$m,𝓁$ ) similarly to the GPBiCG( 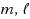$m,𝓁$ ) method proposed by Fujino (2002), can be regarded as an extension of the BiCORSTAB2 method introduced by Zhao and Huang (2013). Inspired by Fujino’s idea for improving the BiCGSTAB2 method, in the established GPBiCOR( 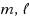$m,𝓁$ ) method the parameters computed by the BiCORSTAB method are chosen at successive 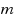$m$ iteration steps, and afterwards the parameters of the GPBiCOR method are utilized in the subsequent 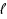$𝓁$ iteration steps. Therefore, the proposed method can inherit the low computational cost of BiCORSTAB and the attractive convergence of GPBiCOR. Extensive numerical convergence results on selected real and complex matrices are shown to assess the performances of the proposed GPBiCOR( 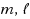$m,𝓁$ ) method, also against other popular non‐Hermitian Krylov subspace methods.