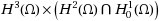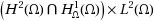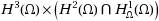Random attractors for the extensible suspension bridge equation with white noise

This paper is devoted to the dynamical behavior of a stochastic extensible suspension bridge equation with white noise. For a deterministic suspension bridge equation, there are many classical results such as existence and uniqueness of a solution and long‐term behavior of solutions. To the best of our knowledge, the existence of attractors for the suspension bridge equation with white noise was not yet considered. We intend to investigate these problems. We first obtain the dissipativeness of a solution in higher‐energy spaces $H^3\left(\Omega \right)\times (H^2\left(\Omega \right)\cap H_0^1\left(\Omega \right))$ . This implies that the random dynamical system generated by the equation has a random attractor in $(H^2\left(\Omega \right)\cap H_{\mathrm{\Omega }}^1\left(\Omega \right))\times L^2\left(\Omega \right)$ , which is a tempered random set in the space in $H^3\left(O\right)\times (H^2\left(O\right)n{H}_0^1\left(O\right))$ .