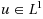| Article ID: | iaor201527803 |
| Volume: | 70 |
| Issue: | 7 |
| Start Page Number: | 1606 |
| End Page Number: | 1639 |
| Publication Date: | Oct 2015 |
| Journal: | Computers and Mathematics with Applications |
| Authors: | Melenk J M, Karkulik M |
| Keywords: | regularisation techniques, smoothing |
We develop a regularization operator based on smoothing on a spatially varying length scale. This operator is defined for functions