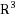The present work is devoted to an approximation of the statistical moments of the solution of a class of elliptic transmission problems in
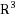with uncertainly located transmission interfaces. In this model, the diffusion coefficient has a jump discontinuity across the random transmission interface which models linear diffusion in two different media separated by an uncertain surface. We apply the shape calculus approach to approximate the solution perturbation by the so‐called shape derivative. Correspondingly, statistical moments of the solution are approximated by the moments of the shape derivative. We characterize the shape derivative as a solution of a related homogeneous transmission problem with nonzero jump conditions, which is solved by the boundary integral equation method. A rigorous theoretical framework is developed, and the theoretical findings are supported by and illustrated in two particular examples.
