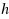Contact problems in solid mechanics are traditionally solved using the
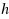‐version of the finite element method. The constraints are enforced along the surfaces of e.g. elastic bodies under consideration. Standard constraint algorithms include penalty methods, Lagrange multiplier methods and combinations thereof. For complex scenarios, a major part of the solution time is taken up by operations to identify points that come into contact. This paper presents a novel approach to model frictionless contact using high order finite elements. Here, we employ an especially designed material model that is inserted into two‐ respectively three‐dimensional regions surrounding contacting bodies. Contact constraints are thus enforced on the same manifold as the accompanying structural problem. The application of the current material formulation leads to a regularization of the Karush–Kuhn–Tucker conditions. Our formulation can be classified as a barrier‐type method. Results are obtained for two‐ and three‐dimensional problems, including a Hertzian contact problem. Comparisons to a commercial FEA package are provided. The proposed formulation works well for non‐matching discretizations on adjacent contact interfaces and handles self‐contact naturally. Since the non‐penetrating conditions are solved in a physically consistent manner, there is no need for an explicit contact search.
