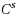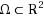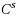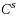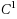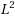| Article ID: | iaor201527727 |
| Volume: | 70 |
| Issue: | 7 |
| Start Page Number: | 1518 |
| End Page Number: | 1538 |
| Publication Date: | Oct 2015 |
| Journal: | Computers and Mathematics with Applications |
| Authors: | Kapl Mario, Vitrih Vito, Jttler Bert, Birner Katharina |
| Keywords: | Poisson's equation |
We study the linear space of