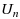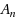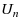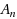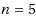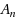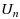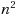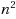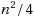| Article ID: | iaor201527236 |
| Volume: | 115 |
| Issue: | 10 |
| Start Page Number: | 779 |
| End Page Number: | 785 |
| Publication Date: | Oct 2015 |
| Journal: | Information Processing Letters |
| Authors: | Nandi Mrinal |
| Keywords: | Fourier transform |
In this paper we have studied the commutative properties of general Discrete Fourier Transform (DFT) matrices