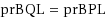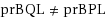| Article ID: | iaor201527220 |
| Volume: | 115 |
| Issue: | 10 |
| Start Page Number: | 750 |
| End Page Number: | 753 |
| Publication Date: | Oct 2015 |
| Journal: | Information Processing Letters |
| Authors: | Doron Dean, Ta-Shma Amnon |
| Keywords: | counting process, statistics (spatial) |
It was recently shown that