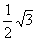| Article ID: | iaor19931505 |
| Country: | Netherlands |
| Volume: | 57 |
| Issue: | 2 |
| Start Page Number: | 193 |
| End Page Number: | 202 |
| Publication Date: | Nov 1992 |
| Journal: | Mathematical Programming |
| Authors: | Du Ding-Zhu, Zhang Yanjun |
| Keywords: | heuristics |
Finding a shortest network interconnecting a given set of points in a metric space is called the Steiner minimum tree problem. The Steiner ratio is the largest lower bound for the ratio between lengths of a Steiner minimum tree and a minimum spanning tree for the same set of points. In this paper, the authors show that in a metric space, if the Steiner ratio is less than one and finding a Steiner minimum tree for a set of size bounded by a fixed number can be performed in polynomial time, then there exists a polynomial-time heuristic for the Steiner minimum tree problem with performance ratio bigger than the Steiner ratio. It follows that in the Euclidean plane, there exists a polynomial-time heuristic for Steiner minimum trees with performance ratio bigger than