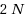| Article ID: | iaor20162452 |
| Volume: | 81 |
| Issue: | 1 |
| Start Page Number: | 1 |
| End Page Number: | 15 |
| Publication Date: | Jun 2016 |
| Journal: | Theory and Decision |
| Authors: | Althfer Ingo, Thiele Raphael |
| Keywords: | decision theory |
The agents of a jury have to decide between a good and a bad option through simple majority voting. In this paper the jury consists of