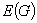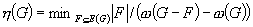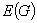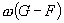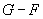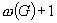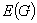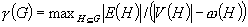| Article ID: | iaor19931441 |
| Country: | Netherlands |
| Volume: | 40 |
| Issue: | 3 |
| Start Page Number: | 284 |
| End Page Number: | 302 |
| Publication Date: | Dec 1992 |
| Journal: | Discrete Applied Mathematics |
| Authors: | Catlin Paul A., Grossman Jerrold W., Hobbs Arthur M., Lai Hong-Jian |
| Keywords: | engineering |
In a 1983 paper, D. Gusfield introduced a function which is called the