We consider an asymmetric inclusion process, which can also be viewed as a model of n queues in series. Each queue has a gate behind it, which can be seen as a server. When a gate opens, all customers in the corresponding queue instantaneously move to the next queue and form a cluster with the customers there. When the nth gate opens, all customers in the nth site leave the system. For the case where the gate openings are determined by a Markov renewal process, and for a quite general arrival process of customers at the various queues during intervals between successive gate openings, we obtain the following results: (i) steady‐state distribution of the total number of customers in the first k queues,
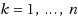; (ii) steady‐state joint queue length distributions for the two‐queue case. In addition to the case that the numbers of arrivals in successive gate opening intervals are independent, we also obtain explicit results for a two‐queue model with renewal arrivals.
