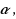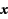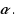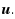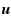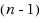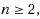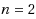| Article ID: | iaor20163645 |
| Volume: | 66 |
| Issue: | 2 |
| Start Page Number: | 311 |
| End Page Number: | 329 |
| Publication Date: | Oct 2016 |
| Journal: | Journal of Global Optimization |
| Authors: | Belotti Pietro, Adams Warren, Shen Ruobing |
| Keywords: | combinatorial optimization |
Given a