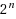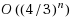An optimal algorithm for Global Optimization and adaptive covering

The general class of zero‐order Global Optimization problems is split into subclasses according to a proposed ‘Complexity measure’ and the computational complexity of each subclass is rigorously estimated. Then, the laboriousness (computational demand) of general Branch‐and‐Bound (BnB) methods is estimated for each subclass. For conventional ‘Cubic’ BnB based on splitting an n‐dimensional cube into $2^n$ sub‐cubes, both upper and lower laboriousness estimates are obtained. The value of the Complexity measure for a problem subclass enters linearly into all complexity and laboriousness estimates for that subclass. A new BnB method based on the lattice $A_n^{\ast }$ is presented with upper laboriousness bound that is, though conservative, smaller by a factor of $O({(4/3)}^n)$ than the lower bound of the conventional method. The optimality of the new method is discussed. All results are extended to the class of Adaptive Covering problems–that is, covering of a large n‐dimensional set by balls of different size, where the size of each ball is defined by a locally computed criterion.