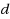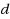Surrogate-RLT cuts for zero‐one integer programs

In this paper, we consider the class of 0–1 integer problems and develop an effective cutting plane algorithm that gives valid inequalities called surrogate‐RLT cuts (SR cuts). Here we implement the surrogate constraint analysis along with the reformulation–linearization technique (RLT) to generate strong valid inequalities. In this approach, we construct a tighter linear relaxation by augmenting SR cuts to the problem. The level‐ $d$ SR closure of a 0–1 integer program is the polyhedron obtained by intersecting all the SR cuts obtained from RLT polyhedron formed over each set of $d$ variables with its initial formulation. We present an algorithm for approximately optimizing over the SR closure. Finally, we present the computational result of SR cuts for solving 0–1 integer programming problems of well‐known benchmark instances from MIPLIB 3.0.